On the Boltzmann Equation

Modeling adsorption with lattice Boltzmann equation

---

Free download. Book file PDF easily for everyone and every device. You can download and read online On the Boltzmann Equation file PDF Book only if you are registered here. And also you can download or read online all Book PDF file that related with On the Boltzmann Equation book. Happy reading On the Boltzmann Equation Bookeveryone. Download file Free Book PDF On the Boltzmann Equation at Complete PDF Library. This Book have some digital formats such us :paperbook, ebook, kindle, epub, fb2 and another formats. Here is The CompletePDF Book Library. It's free to register here to get Book file PDF On the Boltzmann Equation Pocket Guide.

The state of the particle corresponds to a single point in this space, while a system with particles is represented by a set of points. In order to provide a pictorial view, we limit ourselves to a one-dimensional 1D space coordinate and one velocity component. This representation can also be considered as the projection of the entire volume in the two-dimensional 2D plane x , v x.

The ensemble of points changes its shape, as can be observed in figure 1. The acceleration originates from two contributions. This approach, successfully applied to predict the orbit of planets in the solar system, in principle allows one to determine exactly the evolution of any N -particle system, such as a matter in the gas phase. In practice, the number of molecules in a macroscopic system and the uncertainty in the initial conditions 1 make such a deterministic procedure unfeasible for any numerical simulation, even for modern high-performance computers.

Figure 1. Projection of the phase space , on the 2D plane x , v x of an -particle system.

Issues in Solving the Boltzmann Equation for Aerospace Applications

Evolution of the sampling points with left and the starting distribution with the projection of a sampling volume , right. An alternative approach is to describe the evolution of an N -particle system by using the laws of statistics, developing the theory of physical kinetics. Let us consider the following assumptions:. As a first step, let us limit ourselves to a system of free particles moving in an external field, without collisions. In a infinitesimal hypercube identified by the vertices , and , , see figure 1.

Let us now evaluate the rate at which the number of particles inside the sampling volume changes. It corresponds to the flux of particles crossing the surface of the hypercube. For the sake of simplicity, the discussion is restricted to the 2D problem depicted in figure 1. Combining the terms in equations 1. Considering that the sampling volume in the phase space is small, the parentheses on the right-hand side in equation 1.

These assumptions, together with equation 1. The square parentheses in equation 1.

Let us now describe the contribution of collisions to the evolution of the distribution in the phase space. If the gas density is sufficiently small only binary encounters can be considered. If the mean free path is much larger than the interaction distance, these encounters can be treated as collisions.

In a collision at given particle velocities, the final state is completely determined by the deflection angle and, in the case of internal excitation and chemical reactions, by the energy necessary to activate the considered process. The uncertainty in assigning position and speed to the colliding particles makes it necessary to describe the collisions statistically. The cross section of a process is the measure of the probability of a collision output. Let us define the following quantities:. Including the collisional operator, equation 1. Let us construct the collisional operator analyzing the binary encounter sketched in figure 1.

Boltzmann (Kinetic) Equation

In a sampling volume given by equation 1. Equation 1. To have the total number of particles deflected in the given direction we have to multiply this quantity by the number of scattering centers, i. It should be noted that equation 1. The variation expressed by equation 1.

At the same time, the gain rates coming from the reverse process must be considered, as illustrated in figure 1. However, to maintain parity with respect to space—time inversion, the probability of a process must be equal to that of its reverse, i. Scheme of a binary elastic collision left with the deflection angle and a picture of the reverse process right obtained by reversing time and space. The number of particles, all with the same velocity relative to the scattering center blue dot , flowing through the surface in the time interval are those contained in the volume.

Considering as the differential cross section, all these particles are deflected in the same solid angle with velocity. This equation is known as a micro-reversibility principle. This assumption can be demonstrated for collisions with spherical symmetry but it cannot be proved in general. For strange geometries, such as those of large organic molecules, the micro-reversibility principle is not valid.

Nonetheless, in this book the micro-reversibility principle is considered as valid. The micro-reversibility principle has a corresponding law from the macroscopic point of view, the detailed balance principle. The global variation of the distribution function of f A is obtained by summing over all the collision partners B , integrating over all its initial states and over all the final states of A , thus obtaining the final expression for the collisional operator. It is straightforward to demonstrate that in equilibrium, i.

Another important result, obtained for the first time by Boltzmann, is the demonstration of the growth of entropy for an isolated rarefied gas, namely, the H-theorem. Let us define the functional. Substituting the Boltzmann equation see equation 1. Distinguishing the colliders as in the previous section we obtain. The argument of the integral in equation 1. As a consequence of the micro-reversibility principle, the integral must be the same when the initial and final states are exchanged. The integral of a negative function is always negative, it is.

The above theory cannot be applied for ionized gases, as they involve the Coulomb interaction, a long-range force.

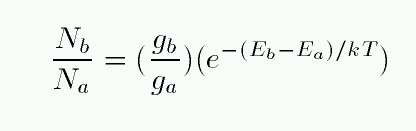
As a consequence charge—charge interaction cannot be treated as a collision. If the gas is weakly ionized, the charge—charge interactions are negligible with respect to collisions with neutrals, but for highly ionized gases the Coulomb forces provide the dominant contribution, and some adjustments are necessary for the Boltzmann equation to be applied to plasmas.

Let us consider a test particle s with charge q s , position in a plasma in stationary conditions. The s particle will feel the electric field produced by all the other charges. We can separate two contributions to , a constant mean field. The time interval must be a macroscopic time, i. In principle, is a continuous function of time, with rapid oscillations with mean time amplitude of the order of. This means that if we sample this field periodically, at successive equal time intervals of amplitude , much larger than , i. If the system is not in a stationary condition, the above assumptions remain valid if the sampling time is small with the respect to the evolution time of whole system, i.

Similar arguments can be used for the magnetic field. This property of the local field suggests that the mean field contributes to the acceleration in the Boltzmann equation, while must contribute to the collision integral, due its random evolution. The mean field does not produce entropy, a consequence of the H -theorem, differently from the random field.

In fully ionized gases it could be demonstrated that the entropy variation due to collisions is much slower than other macroscopic quantities such as charge density ,. The Boltzmann equation in equation 1. This system is known as the Vlasov equation. In most practical applications the time derivatives of the fields in the Maxwell equations are negligible, and the quasi-static fields are considered. The validity of the Vlasov equation depends on two conditions:.

The collisional term in the Boltzmann equation results from the dynamics of binary collisions in the plasma promoting elastic, inelastic, and reactive processes that govern the temporal evolution of the kinetics at a microscopic level. The construction of a reliable database for the elementary probabilities represents a challenge even today, due to the requirements of accuracy, consistency, and completeness, issues that significantly affect the predictive capability of kinetic models, not only in the estimation of macroscopic plasma parameters, but also in shedding light on relevant collisional mechanisms [ 18 ].

Modern approaches in quantum molecular dynamics are fully exploited to aim for the highest accuracy. However, the wide spectrum of theoretical methods, including semiclassical, quasi-classical, classical, and semi-empirical, provides methods that are suitable for specific classes of processes, offering a favorable balance between the reliability of dynamics information and the computational load characterizing the derivation of a complete dataset.

This is, in particular, the case for state-to-state kinetics see section 8. Elastic collisions usually dominate the kinetics and fully determine the transport properties of thermal equilibrium plasmas [ 6 ]. Transport cross sections, i.

Boltzmann equation

The interaction potential from accurate electronic structure calculations, or modeled with either full-range analytical forms [ 6 ] or a phenomenological potential [ 22 ], is assumed to be isotropic, so is dependent only on the approaching line of colliding partners, also for interactions involving molecules. Some examples do exist in the literature of classical trajectory calculations on ab initio surfaces for molecular collisions [ 23 ], considering anisotropic potentials, however, for small rapidly rotating molecules an isotropic angle-averaged potential can be assumed [ 24 ].

A rigorous quantum coupled-channel approach [ 20 ] is required; however, it is worth mentioning the asymptotic approach [ 25 , 26 ], based on the idea of expanding the cross section in terms of small parameters connected to the geometry of the collision.

Deviations from the ideal model

In the case of electron elastic scattering, the quantum nature of the interactions is not negligible and manifests itself in the features of the energy profile of the cross section, as the low-energy peaks due to resonances, or the Ramsauer minimum [ 27 ]. Therefore a quantum approach is required and the collision integrals are evaluated by integration of theoretical [ 28 ] or experimental differential elastic electron-scattering cross sections. Inelastic and reactive channels are considered negligible in transport, except for quantum effects at low temperatures.

However, they play a key role in non-equilibrium plasmas, chemical species undergoing excitation, and dissociation and ionization processes induced by electron impact or collisions with heavy particles with increasing threshold energies. Quantum approaches the R-matrix [ 29 ], close-coupling, the Schwinger multi-channel [ 30 ], local complex potential [ 31 ] represent the best theoretical framework for the investigation of the dynamics in electron—molecule scattering. They involve non-adiabatic effects as the resonant electron capture with the formation of long-living negative ion intermediates or vibrionic coupling.

However, other methods have been successfully used in the past: first-order approaches, such as the Born, Born—Bethe, and Born—Ochkur approaches [ 32 ], which are accurate for high collision energies; semiclassical methods [ 33 — 35 ] that assume that the impinging electron moves classically in linear trajectories and the quantum molecular target; and the classical Gryzinskii method [ 36 ].

Boltzmann equation - Wikipedia

More recently, novel simplified approaches have been proposed in the literature, such as the BE f -scaling method [ 37 ], based on a rescaling procedure of the Born cross section for dipole-allowed vibrionic excitations with the experimental optical oscillator strengths, and the similarity approach [ 38 ] or the binary encounter dipole BED model for ionization [ 39 , 40 ].

Simplified approaches are still attractive, demonstrating in many cases striking agreement with experiments and representing very promising tools for more complex molecular systems. For the dynamics of heavy-particle collisions, leading to energy transfer among internal and translation degrees of freedom of colliding partners, rearrangement reactions, or dissociation, the quasi-classical trajectory QCT method [ 18 , 41 , 42 ] has been well assessed.

It has proved to compare well with and complement the quantum approaches [ 43 ].

• The Person Behind the Syndrome
• Both Sides of the Mirror: The Science and Art of Ballet (A Dance Horizons Book)
• Afghanistan: The Soviet Invasion and the Afghan Response, 1979-1982
• The Meaning Of Language
• Crossing the Digital Divide: Race, Writing, and Technology in the Classroom (Language and Literacy Series)
• Joy of Cooking: All About Party Foods & Drinks
• Metal Powders. A Global Survey of Production, Applications and Markets to 2010