Statistical Tables: Explained and Applied
Free download. Book file PDF easily for everyone and every device. You can download and read online Statistical Tables: Explained and Applied file PDF Book only if you are registered here. And also you can download or read online all Book PDF file that related with Statistical Tables: Explained and Applied book. Happy reading Statistical Tables: Explained and Applied Bookeveryone. Download file Free Book PDF Statistical Tables: Explained and Applied at Complete PDF Library. This Book have some digital formats such us :paperbook, ebook, kindle, epub, fb2 and another formats. Here is The CompletePDF Book Library. It's free to register here to get Book file PDF Statistical Tables: Explained and Applied Pocket Guide.
Contents:
First, and most important, social network analysis is about relations among actors, not about relations between variables. Most social scientists have learned their statistics with applications to the study of the distribution of the scores of actors cases on variables, and the relations between these distributions. We learn about the mean of a set of scores on the variable "income. The application of statistics to social networks is also about describing distributions and relations among distributions.
But, rather than describing distributions of attributes of actors or "variables" , we are concerned with describing the distributions of relations among actors.
- Introduction to social network analysis: Chapter Some statistical tools.
- Learn from the Grandmasters.
- What are Basic Statistics.
In applying statistics to network data, we are concerned the issues like the average strength of the relations between actors; we are concerned with questions like "is the strength of ties between actors in a network correlated with the centrality of the actors in the network? Second, many of tools of standard inferential statistics that we learned from the study of the distributions of attributes do not apply directly to network data. Most of the standard formulas for calculating estimated standard errors, computing test statistics, and assessing the probability of null hypotheses that we learned in basic statistics don't work with network data and, if used, can give us "false positive" answers more often than "false negative".
This book contains several new or unpublished tables, such as one on the significance of the correlation coefficient r, one giving the percentiles of the Ē2 statistic. Buy Statistical Tables, Explained and Applied by Louis Laurencelle, Francois-A. Dupuis, Les Edition le Griffon d'Argile (ISBN: ) from Amazon's.
This is because the "observations" or scores in network data are not "independent" samplings from populations. In attribute analysis, it is often very reasonable to assume that Fred's income and Fred's education are a "trial" that is independent of Sue's income and Sue's education.
We can treat Fred and Sue as independent replications. In network analysis, we focus on relations, not attributes. So, one observation might well be Fred's tie with Sue; another observation might be Fred's tie with George; still another might be Sue's tie with George. These are not "independent" replications.
Applied Statistics for the Six Sigma Green Belt
Fred is involved in two observations as are Sue an George , it is probably not reasonable to suppose that these relations are "independent" because they both involve George. The standard formulas for computing standard errors and inferential tests on attributes generally assume independent observations. Applying them when the observations are not independent can be very misleading. Instead, alternative numerical approaches to estimating standard errors for network statistics are used.
These "boot-strapping" and permutations approaches calculate sampling distributions of statistics directly from the observed networks by using random assignment across hundreds or thousands of trials under the assumption that null hypotheses are true. These general points will become clearer as we examine some real cases. So, let's begin with the simplest univariate descriptive and inferential statistics, and then move on to somewhat more complicated problems. For most of the examples in this chapter, we'll focus again on the Knoke data set that describes the two relations of the exchange of information and the exchange of money among ten organizations operating in the social welfare field.
Figure These particular data happen to be asymmetric and binary. Most of the statistical tools for working with network data can be applied to symmetric data, and data where the relations are valued strength, cost, probability of a tie. As with any descriptive statistics, the scale of measurement binary or valued does matter in making proper choices about interpretation and application of many statistical tools. The data that are analyzed with statistical tools when we are working with network data are the observations about relations among actors.
If data are symmetric i. What we would like to summarize with our descriptive statistics are some characteristics of the distribution of these scores. Univariate descriptive statistics for Knoke information and money whole networks. For the information sharing relation, we see that we have 90 observations which range from a minimum score of zero to a maximum of one. Since the relation has been coded as a "dummy" variable zero for no relation, one for a relation the mean is also the proportion of possible ties that are present or the density , or the probability that any given tie between two random actors is present Several measures of the variability of the distribution are also given.
The sums of squared deviations from the mean, variance, and standard deviation are computed -- but are more meaningful for valued than binary data. The Euclidean norm which is the square root of the sum of squared values is also provided. This suggests quite a lot of variation as a percentage of the average score. A quick scan tells us that the mean or density for money exchange is lower, and has slightly less variability. In addition to examining the entire distribution of ties, we might want to examine the distribution of ties for each actor.
In Statistics
Since the relation we're looking at is asymmetric or directed, we might further want to summarize each actor's sending row and receiving column. Figures We see that actor 1 COUN has a mean or density of tie sending of. That is, this actor sent four ties to the available nine other actors. Actor 1 received somewhat more information than they sent, as their column mean is. In scanning down the column in figure With valued data, the means produced index the average strength of ties, rather than the probability of ties. With valued data, measures of variability may be more informative than they are with binary data since the variability of a binary variable is strictly a function of its mean.
The main point of this brief section is that when we use statistics to describe network data, we are describing properties of the distribution of relations, or ties among actors -- rather than properties of the distribution of attributes across actors. The basic ideas of central tendency and dispersion of distributions apply to the distributions of relational ties in exactly the same way that they do to attribute variables -- but we are describing relations, not attributes.
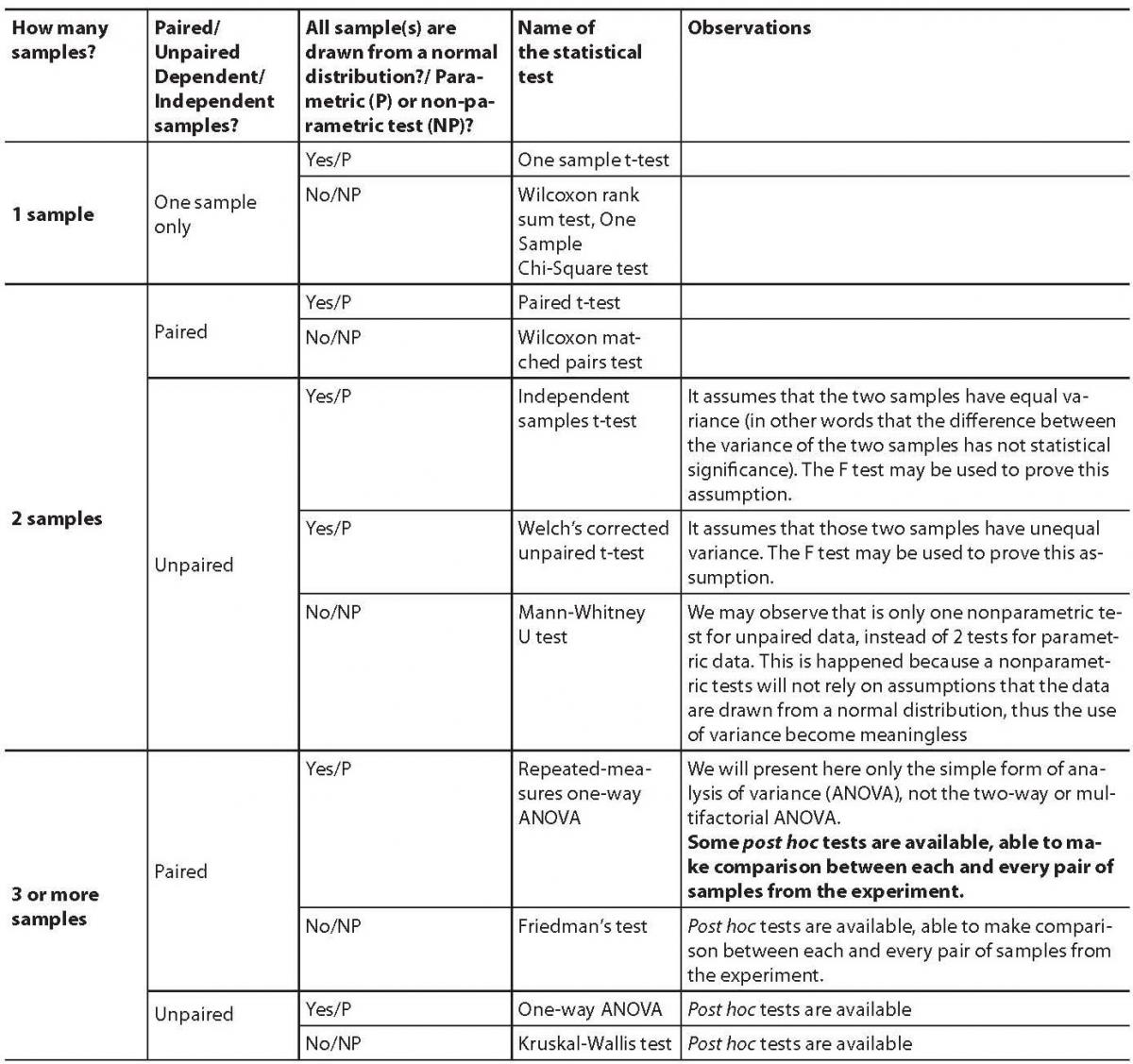
Comparing groups for statistical differences: how to choose the right statistical test?
Of the various properties of the distribution of a single variable e. If we are working with the distribution of relations among actors in a network, and our measure of tie-strength is valued, central tendency is usually indicated by the average strength of the tie across all the relations. We may want to test hypotheses about the density or mean tie strength of a network.
In the analysis of variables, this is testing a hypothesis about a single-sample mean or proportion. We might want to be confident that there actually are ties present null hypothesis: network density is really zero, and any deviation that we observe is due to random variation. We might want to test the hypothesis that the proportion of binary ties present differs from. Let's suppose that I think that all organizations have a tendency to want to directly distribute information to all others in their field as a way of legitimating themselves.
If this theory is correct, then the density of Knoke's information network should be 1. We can see that this isn't true. The "Expected density" is the value against which we want to test. Here, we are asking the data to convince us that we can be confident in rejecting the idea that organizations send information to all others in their fields. The parameter "Number of samples" is used for estimating the standard error for the test by the means of "bootstrapping" or computing estimated sampling variance of the mean by drawing random sub-samples from our network, and constructing a sampling distribution of density measures.
Looking at percentile 90, which stands for a significance level a of 0. The binomial distribution for this case is illustrated in Figure 2. Correlations in Non-homogeneous Groups. These differences do not constitute a revision. An important aspect of the "description" of a variable is the shape of its distribution, which tells you the frequency of values from different ranges of the variable. Therefore you could:.
The sampling distribution of a statistic is the distribution of the values of that statistic on repeated sampling. The standard deviation of the sampling distribution of a statistic how much variation we would expect to see from sample to sample just by random chance is called the standard error. We see that our test value was 1.
If we used this for our test, the test statistic would be -. However, if we use the bootstrap method of constructing networks by sampling random sub-sets of nodes each time, and computing the density each time, the mean of this sampling distribution turns out to be. Using this alternative standard error based on random draws from the observed sample, our test statistic is Why do this? The classical formula gives an estimate of the standard error. This is because the standard formula is based on the notion that all observations i. But, since the ties are really generated by the same 10 actors, this is not a reasonable assumption.
Using the actual data on the actual actors -- with the observed differences in actor means and variances, is a much more realistic approximation to the actual sampling variability that would occur if, say, we happened to miss Fred when we collected the data on Tuesday. In general, the standard inferential formulas for computing expected sampling variability i.
Using them results in the worst kind of inferential error -- the false positive, or rejecting the null when we shouldn't. The basic question of bivariate descriptive statistics applied to variables is whether scores on one attribute align co-vary, correlate with scores on another attribute, when compared across cases.
The basic question of bivariate analysis of network data is whether the pattern of ties for one relation among a set of actors aligns with the pattern of ties for another relation among the same actors. That is, do the relations correlate? Three of the most common tools for bivariate analysis of attributes can also be applied to the bivariate analysis of relations:.
Does the central tendency of one relation differ significantly from the central tendency of another? For example, if we had two networks that described the military and the economic ties among nations, which has the higher density? Are military or are economic ties more prevalent? This kind of question is analogous to the test for the difference between means in paired or repeated-measures attribute analysis. Is there a correlation between the ties that are present in one network, and the ties that are present in another? For example, are pairs of nations that have political alliances more likely to have high volumes of economic trade?
This kind of question is analogous to the correlation between the scores on two variables in attribute analysis.
If we know that a relation of one type exists between two actors, how much does this increase or decrease the likelihood that a relation of another type exists between them? For example, what is the effect of a one dollar increase in the volume of trade between two nations on the volume of tourism flowing between the two nations? This kind of question is analogous to the regression of one variable on another in attribute analysis. In the section above on univariate statistics for networks, we noted that the density of the information exchange matrix for the Knoke bureaucracies appeared to be higher than the density of the monetary exchange matrix.

That is, the mean or density of one relation among a set of actors appears to be different from the mean or density of another relation among the same actors. When both relations are binary, this is a test for differences in the probability of a tie of one type and the probability of a tie of another type. When both relations are valued, this is a test for a difference in the mean tie strengths of the two relations.
Let's perform this test on the information and money exchange relations in the Knoke data, as shown in Figure Test for the difference of density in the Knoke information and money exchange relations. Results for both the standard approach and the bootstrap approach this time, we ran 10, sub-samples are reported in the output.