Trigonometry

Trigonometry Formula
Free download. Book file PDF easily for everyone and every device. You can download and read online Trigonometry file PDF Book only if you are registered here. And also you can download or read online all Book PDF file that related with Trigonometry book. Happy reading Trigonometry Bookeveryone. Download file Free Book PDF Trigonometry at Complete PDF Library. This Book have some digital formats such us :paperbook, ebook, kindle, epub, fb2 and another formats. Here is The CompletePDF Book Library. It's free to register here to get Book file PDF Trigonometry Pocket Guide.

Contents:

  • Navigation menu
  • Course summary
  • Trigonometry Calculator - Symbolab
  • Navigation menu
  • Trigonometry

    • Navigation menu

    Learn more about Trigonometric Ratios here in detail. Now let us start with the basic formulas of trigonometry and see the basic relationships on which the whole concept is based on. In a right-angled triangle, we have Hypotenuse, Base and Perpendicular. The longest side is known as the hypotenuse, the other side which is opposite to the angle is Perpendicular and the third side is Base.

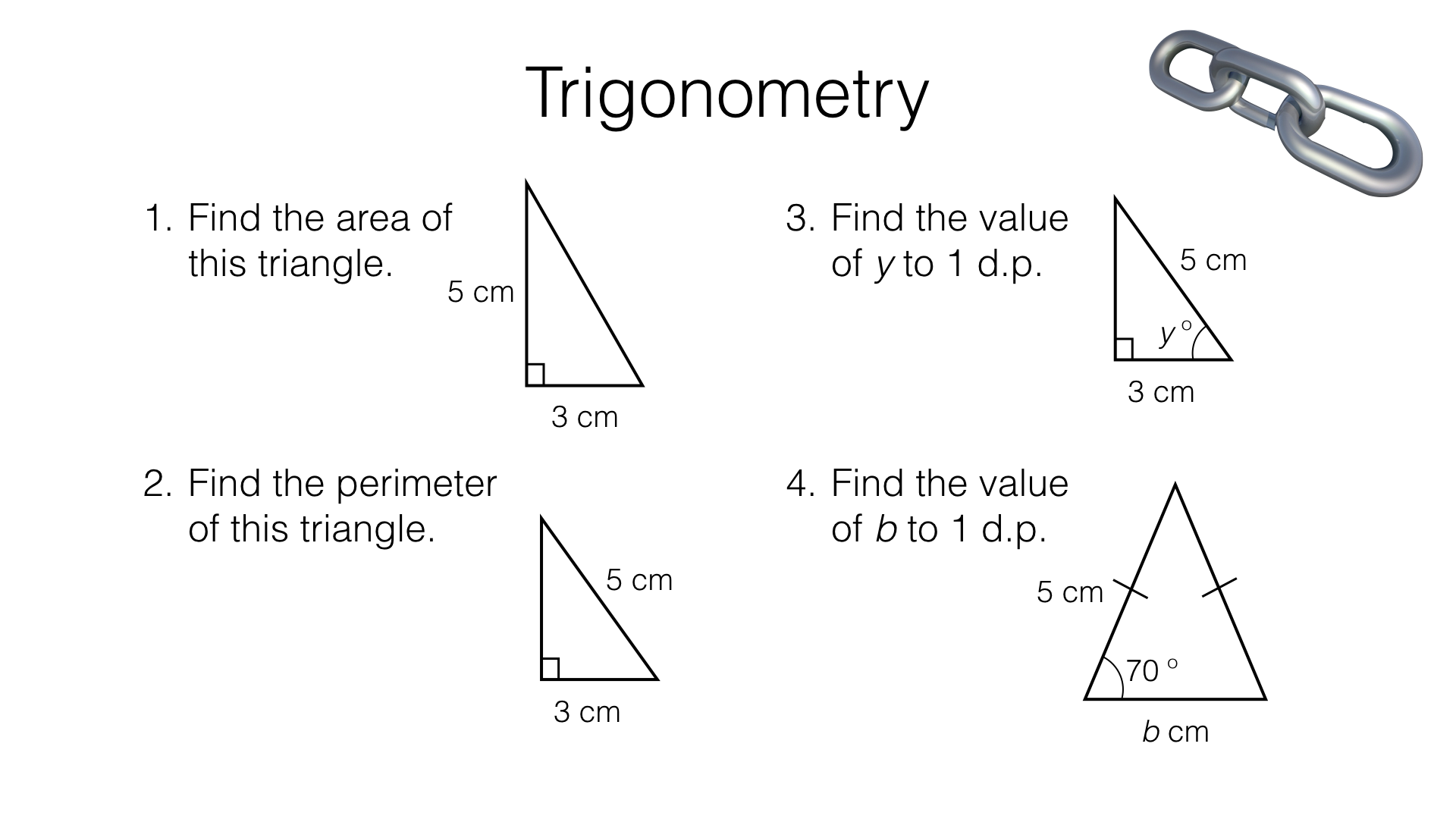
    Read this book

    The six trigonometric functions are sine, cosine, secant, cosecant, tangent and cotangent. So now all the trigonometric ratios are based on the lengths of these lengths of the side of the triangle and the angle of the triangle. The basic trigonometric identities based on the Pythagoras Theorem are listed here. You can use the basic definition and Pythagoras theorem to prove these.

    Course summary

    Trigonometry is a branch of mathematics that studies relationships between side lengths and angles of triangles. The field emerged in the Hellenistic world. Trigonometry (from Greek trigonon "triangle" + metron "measure"). Want to learn Trigonometry? Here is a quick summary. Follow the links for more, or go to.

    Trigonometric ratios for negative angles can be derived using the circular concept of negative angles and can be derived using cartesian notation and conventions. If the angles are given in any of the four quadrants then the angle can be reduced to the equivalent first quadrant by changing signs and trigonometric ratios:.

    And from the above identities we can derive the multiplication rules and the summation rules of two trigonometric ratios:. The trigonometric equations can also be related to complex numbers and through the following relations:.

    Trigonometry Calculator - Symbolab

    If you are listening to these videos on headphones, you may want to consider setting your sound channels to come through both sides. This document will give you an idea of how to accomplish that. First Chapter: Trigonometric Functions 1. Plane Trigonometry, rev. Dubuque, IA: Wm.

    Brown, Robinson, R. Monthly 64 , , Siddons, A. Trigonometry, Part I.

    London: Cambridge University Press, a. Trigonometry, Part II.

    London: Cambridge University Press, b. Trigonometry, Part III. London: Cambridge University Press, c. Trigonometry, Part IV.

    Navigation menu

    Home - Education Resources. Monthly 64 , , Osborn's rule gives a prescription for converting trigonometric identities to analogous identities for hyperbolic functions. Walk through homework problems step-by-step from beginning to end. The ratio of the two sides a is the same as the ratio of the two sides b and is also the same as the two sides c. The leaning ladder used to put up the screen must be longer than the screen itself, right? Robinson, R.

    London: Cambridge University Press, d. Sloane, N. Thompson, J. Trigonometry for the Practical Man.

    • Management Education in India: Perspectives and Practices.
    • African-American Religious Leaders.
    • Conditions of Use?
    • Accessibility links?

    Princeton, NJ: Van Nostrand, Yates, R. Ann Arbor, MI: J.

    Trigonometry

    Edwards, pp. Weisstein, E. Zill, D.