Advanced Linear Algebra

MATH 528 - Advanced Linear Algebra

---

Free download. Book file PDF easily for everyone and every device. You can download and read online Advanced Linear Algebra file PDF Book only if you are registered here. And also you can download or read online all Book PDF file that related with Advanced Linear Algebra book. Happy reading Advanced Linear Algebra Bookeveryone. Download file Free Book PDF Advanced Linear Algebra at Complete PDF Library. This Book have some digital formats such us :paperbook, ebook, kindle, epub, fb2 and another formats. Here is The CompletePDF Book Library. It's free to register here to get Book file PDF Advanced Linear Algebra Pocket Guide.

Besides his books for O'Reilly, Dr. Roman has written two other computer books, both published by Springer-Verlag.

Math 4063/5023: Advanced Linear Algebra

Advanced Linear Algebra. Steven Roman. From the reviews of the second edition: "In this 2nd edition, the author has rewritten the entire book and has added more than pages of new materials.

1st Edition

Part IBasic Linear Algebra. Index of Symbols. A set that is not finite is infinite. The cardinal number or cardinality, of a finite set is just the number of elements in the set.

The reader will no doubt recall that the power set P S of a set S is the set of all subsets of S. For finite sets, the power set of S is always bigger than the set itself. You think MAT is not challenging enough. Wait till you have had a quiz, which usually occurs in the 3rd week. Instead see if you can produce correct solutions to most of the problems in the allotted time.

You should have some solid experience writing proofs to do well in MAT File Attachments. MAT Sample Problems. Keep an open mind and seek advice to help you reach your goals!

Lots of help is available if you run into unexpected difficulty. Early action can make a big difference! It is easy to switch down to after a few weeks. The grading scheme takes into account that is harder than Take the course that matches your current knowledge.

Trying to jump ahead can actually slow you down. This approach is evident even in the very first chapter, on vector spaces and linear transformations.

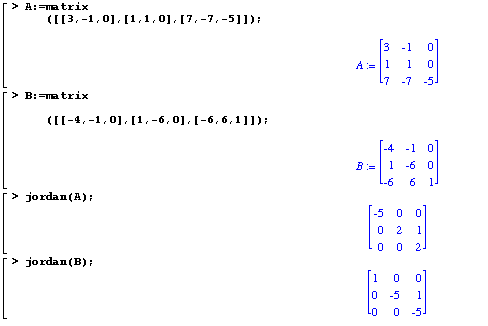
Vector spaces are not assumed finite-dimensional, and are defined over an arbitrary field rather than the field of real or complex numbers. It is shown that a volume function exists and is unique up to scaling, and the determinant of a square matrix A is defined to be the image of A under that volume function scaled, of course, so that the volume of the unit n-cube is 1.

This definition is immediately followed by two sections, giving a more traditional characterization of determinants and setting out the basic facts about them.

(PDF) Advanced Linear Algebra (Third Edition) by Steven Roman | Muhsang Sudadama - giuliettasprint.konfer.eu

The chapter then concludes with three sections discussing topics not generally seen in elementary courses: the first discusses determinants and invertibility of integer matrices, the second discusses orientation in real vector spaces via a detour through the topology of the general linear group in which the connected components of the group GL n R are characterized; knowledge of the topological ideas is assumed , and the third discusses without proof some basic facts about Hilbert matrices.

This approach to determinants reflects a fairly common theme: the author frequently gives nonstandard definitions of topics and then proves the equivalence to the usual definition. For example, to define the product of two matrices A and B of appropriate sizes the author takes the composition of the linear transformations defined by A and B and defines AB to be the matrix corresponding to this composition. Likewise, the transpose of a matrix A is defined as the matrix corresponding to the dual of the transformation induced by A.

Whether any enhanced motivation and insight given by this approach justifies the departure from standard definitions is, of course, a matter of individual taste.

MATH 4377 - Advanced Linear Algebra I & 4378 - Advanced Linear Algebra II

The next two chapters address the structure of linear transformations via eigenvalues and canonical forms. The first of these chapters provides a very succinct and efficient development of eigenvectors and generalized eigenvectors developed in tandem , the minimal and characteristic polynomials of a matrix, diagonalizability and triangularizability, and then culminates in a section relating these concepts to the theory of linear differential equations.

The next chapter the longest and, I thought, most difficult addresses the Jordan and rational canonical forms of a matrix. The approach here is by invariant subspaces; in an appendix, the author discusses the module-over-a-PID approach to this topic. An algorithm for computing the Jordan form of a matrix whose characteristic polynomial is given as the product of linear factors is provided, as are several very helpful, rather non-trivial, examples, worked out in some detail.

MAS 5145 Advanced Linear Algebra and Matrix Theory

It would have been nice, though, to see more applications of the material in this chapter; for example, it would not have taken much additional exposition to prove the interesting result that any square matrix is similar to its transpose, but this does not appear. Chapters 6 and 7 discuss, respectively, forms bilinear, sesquilinear, quadratic and their classification, and inner products on real and complex vector spaces. Unlike many books on quadratic forms e.

• Planning in Intelligent Systems: Aspects, Motivations, and Methods
• Environment, Power, and Society for the Twenty-first Century: The Hierarchy of Energy
• 101 Ways You Can Help: How to Offer Comfort and Support to Those Who Are Grieving
• Certified Ethical Hacker (CEH) Foundation Guide
• The place names of the White Mountains
• Qualitative Research In Intelligence And Marketing